Ahmad, A., Ali, M., Ali, A. H., El-Rahman, M. A., Hincal, E., & Neamah, H. A. (2024). Mathematical analysis with control of liver cirrhosis causing from HBV by taking early detection measures and chemotherapy treatment. Scientific Reports, 14(1), 28463.

This study explores the mechanisms through which the Hepatitis B (HB) virus causes harmful inflammation in the liver, with a focus on early detection and therapy using corticosteroids or chemotherapy. The aim is to develop a deeper understanding of the virus’s impact and the role of intervention strategies in mitigating liver cirrhosis. A novel mathematical model has been created to study the HB virus, considering both asymptomatic individuals and treatment measures that help control the progression to liver cirrhosis. The model is examined quantitatively and qualitatively to determine its stability, with a strong emphasis on assessing boundedness, positivity, existence, uniqueness, and global stability. These components are critical for evaluating the overall effect of the virus in a population and testing the impact of treatment measures, such as chemotherapy.

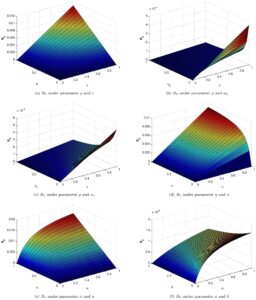
To ensure reliable conclusions, the model’s stability is tested through Lyapunov’s first derivative functions, which help assess global stability. Additionally, the Lipschitz condition is employed to confirm the uniqueness of solutions within the system, and the model’s responses are analyzed under constraints to comprehend the epidemic dynamics effectively. The use of fractional-order modeling techniques (FFO) is key in providing accurate, continuous monitoring of the HBV virus and its effects, particularly in individuals receiving treatment for liver cirrhosis. This approach helps ensure that the environment can be monitored effectively and that treatment measures can be adjusted based on real-time data.

The study also incorporates simulations using MATLAB to observe the behavior of HBV in asymptomatic individuals undergoing chemotherapy. These simulations reveal important insights into the dynamics of the virus and the potential benefits of early detection, asymptomatic measures, and targeted therapy. The results emphasize the importance of preventing the virus from progressing to the chronic stage and reducing the incidence of liver cirrhosis through early intervention strategies.

The research confirms the need for global initiatives to control HBV and liver cirrhosis. The findings suggest that a combination of early detection and treatment measures, including chemotherapy, significantly reduces the spread of the virus. By using fractional values to monitor the virus’s progress, the model provides a dynamic understanding of HBV’s impact on the population and offers valuable projections for future research. These projections can help develop more effective intervention strategies and improve the understanding of HBV’s environmental dissemination, ultimately contributing to more effective control measures for liver cirrhosis and related complications.

 

 

Abstract

Reformulating the physical processes associated with the evolution of different ailments in accordance with globally shared objectives is crucial for deeper comprehension. This study aims to investigate the mechanism by which the HB virus induces harmful inflammation of the liver, with a focus on early detection and therapy using corticosteroids or chemotherapy. Based on the developed hypothesis, a new mathematical model has been created for this purpose. The recently developed system for HBV is SEIR, which is examined both quantitatively and qualitatively to determine its actual effect on stability. Reliable conclusions are ensured by examining the system’s boundedness, positivity, existence, uniqueness, and conducting local and global stability analysis-all crucial components of epidemic models. Global stability is tested using Lyapunov first derivative functions to assess the overall impact of asymptomatic persons and chemotherapy treatment. Additionally, the Lipschitz condition is used to confirm the unique solutions for the newly built HBV model using methods from fixed point theory, thus meeting the requirements for uniqueness and existence. Since the population must maintain this property, positivity is confirmed using global derivatives and Lipschitz criteria to calculate the rate of change in each sub-compartment. Applying the Mittag-Leffler kernel with a fractal-fractional operator to continuously monitor the HBV virus for liver cirrhosis infection yields dependable results. Furthermore, the current situation regarding the HBV outbreak pertaining to liver cirrhosis infection, along with the control measures implemented following early diagnosis through asymptomatic measures and chemotherapy treatment under constant observation, are established to prevent chronic stage infections. Simulations have been used to study the true behavior and impact of HBV in asymptomatic persons receiving chemotherapy for liver cirrhosis infection in the community. This research is essential for understanding the spread of viruses and developing control strategies based on our validated findings to mitigate the risk factors associated with liver cirrhosis.

For further details, access the original paper from the publisher’s link: Mathematical analysis with control of liver cirrhosis causing from HBV by taking early detection measures and chemotherapy treatment